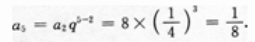2022年05月24日成考高起点每日一练《数学(文史)》

2022年成考高起点每日一练《数学(文史)》5月24日专为备考2022年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、函数y=sin2x的最小正周期是

• A：6π
• B：2π
• C：π
• D：π/2

答 案：C

2、若a，b，C为实数，且a≠o．设甲：b2-4ac≥0，乙：ax²+bx+C-0有实数根， 则 （ ）

• A：甲既不是乙的充分条件，也不是乙的必要条件
• B：甲是乙的必要条件，但不是乙的充分条件
• C：甲是乙的充分必要条件
• D：甲是乙的充分条件，但不是乙的必要条件

答 案：C

解 析：本题主要考查的知识点为简易逻辑．【应试指导】  

3、如果一次函数y=kx+b的图像经过点A（1，7）和B（0，2），则k=

• A：-5
• B：1
• C：2
• D：5

答 案：D

4、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

主观题

1、弹簧的伸长与下面所挂砝码的重量成正比，已知弹簧挂20g重的砝码时长度是12cm，挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度。

答 案：设弹簧原长为y0cm，则弹簧伸长量为(y-y0)cm，由题意得y-y0=kx，即y=kx+y0,

所求函数关系式为y=0.2x+8，弹簧的原长为8cm。

2、已知函数f(x)=x3+x2-5x-1。求：(1)f(x)的单调区间; (2)f(x)零点的个数。

答 案：

3、设函数f（x）=x³-3x²-9x．求 （I）函数f（x）的导数；（II）函数f（x）在区间[1，4]的最大值与最小值．

答 案： 

4、已知抛物线经过点(2，3)，对称轴方程为x=1，且在x轴上截得的弦长为4，试求抛物线的解析式。

答 案：设抛物线y=a(x-x1)(x-x2)，与x轴的两交点为A(x1，0)，B(x2，0)，由｜AB｜=4，对称轴为x=1得x1=1-2=-1，x2=1+2=3，∴y=a(x+1)(x-3)，又∵抛物线过点(2，3)，∴3=a(2+1)(2-3)，得a=-1，故所求的抛物线方程为y=-(x+1)(x-3)，即y=-x²+2x+3。

填空题

1、任选一个不大于20的正整数，它恰好是3的整数倍的概率是（）。

答 案：3/10

解 析：设n为不大于20的正整数的个数，则n=20，m为在这20个数中3的倍数：3、6、9、12、15、18的个数，所以m=6，所求的概率为m/n=6/20=3/10。

2、等比数列{a_n}中，若a₂=8，公比为1/4，则a₅=

答 案：1/8

解 析：【考情点拨】本题主要考查的知识点为等比数列．【应试指导】