2025年05月03日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》5月3日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、下列各等式不成立的是（）。

• A：3^x·2^x=6^x
• B：9^x=（3^x）2
• C：
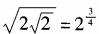
• D：

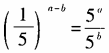
答 案：D

解 析：3^x·2^x=（3·2）^x=6^x，排除A；（3^x）²=（3²）^x=9^x，排除B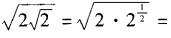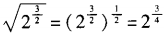；，排除C。选D。  

2、下列四个命题中正确的是（）。 ①已知a，b，c三条直线，其中a，b异面，a//c，则b，c异面。
②若a与b异面，b与c异面，则a与c异面。
③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。
④不同在任何一个平面内的两条直线叫异面直线。

• A：③④
• B：②③④
• C：①②③④
• D：①②

答 案：A

解 析：①b与c可相交，②a与c可以有平行、相交、异面三种位置关系。答案为A。  

3、已知{i，j，k}是单位正交基底，a＝i＋j，b＝－i＋j－k，则a·b＝（）。

• A：-1
• B：1
• C：0
• D：2

答 案：C

解 析：a·b＝（1，1，0）·（－1，1，－1）＝1×（－1）＋1×1＋0×（－1）＝0。答案为C。  

4、中心在坐标原点，一个焦点的坐标是（-3,0），一条渐近线方程式的双曲线方程是（）。

• A：
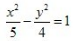
• B：
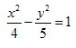
• C：
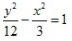
• D：

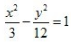
答 案：B

主观题

1、已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图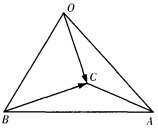）。求证：OA⊥BC。

答 案：

2、已知等差数列前n项和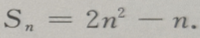 （Ⅰ）求这个数列的通项公式;（Ⅱ）求数列第六项到第十项的和

答 案：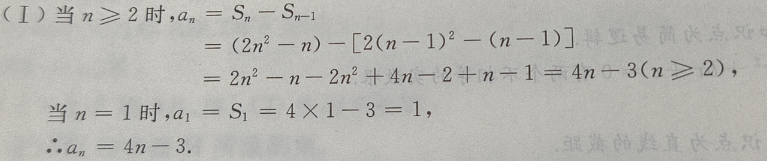  

3、已知数列{a_n}中，a₁=2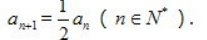， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

答 案：解：

4、计算 （1）tan5°+ cot5°- 2sec80°
（2）tan15°+cot15
（3）sin15°sin75°

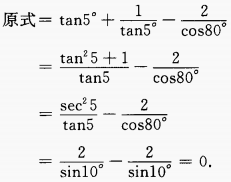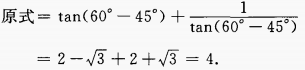答 案：（1）化切割为弦进行运算。 （2） （3）

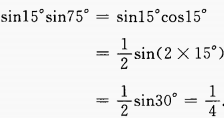
填空题

1、已知角α的终边过点P（-8m，-6cos60°）且cosα=-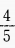，则m______。

答 案：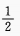

解 析：∵P(-8m,-3)且cosα=∴P点在第三象限 ∴m＞0∵y=-3,r=5∴x=-8m=-4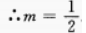

2、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）  

答 案：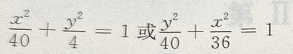

解 析：原直线方程可化为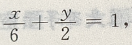交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,