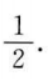2025年05月04日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》5月4日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、顶点在坐标原点，准线方程为y=4的抛物线方程式（）。

• A：
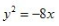
• B：
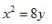
• C：
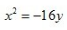
• D：

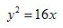
答 案：C

2、函数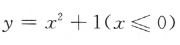的反函数是（）

• A：
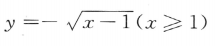
• B：
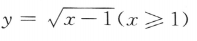
• C：
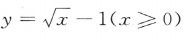
• D：

答 案：A

解 析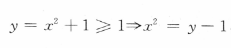：，由于x≤0，故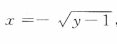把x与y互换，得所求反函数为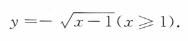

3、下列关系式中，对任意实数A＜B＜0都成立的是（）。

• A：a²＜b²
• B：lg(b－a)＞0
• C：2^a＜2^b
• D：lg(-a)＜lg(－b)

答 案：C

4、已知tanα，tanβ是方程2x²-4x+1=0的两根，则tan（α+β）=（）。

• A：4
• B：-4
• C：
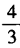
• D：8

答 案：A

解 析：由已知，得tanα+tanβ==2，tanαtanβ=，所以  

主观题

1、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得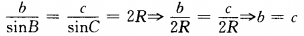

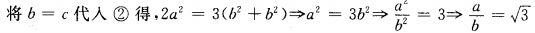
∴a：b=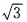：1
于是a：b：c=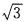：1：1。  

2、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

3、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：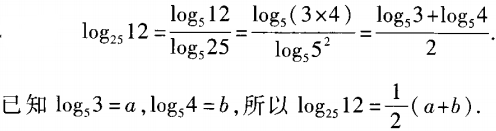

4、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：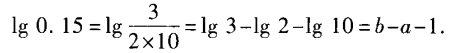

填空题

1、已知函数y=a²+bx+c的图像是以(6,-12)为顶点的抛物线，并且与x轴的一个交点坐标是(8,0)，则a=()，b=()，c=()

答 案：  3；-36；96  

解 析：根据顶点坐标是（6，-12），设y=a(x-6)²-12(8,0)代入得：0=a*(8-6)²-12得到a=3
即y=3(x-6)²-12=3x²-36x+96
故a=3,b=-36,c=96

2、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：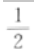

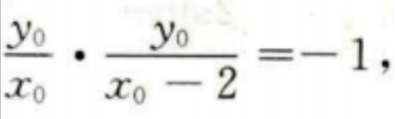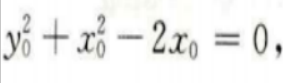
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以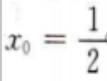故切点横坐标为