2025年06月08日成考专升本每日一练《高等数学二》

2025年成考专升本每日一练《高等数学二》6月8日专为备考2025年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：

单选题

1、设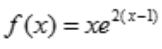，则在x＝1处的切线方程是（）.

• A：
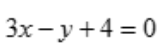
• B：
• C：
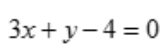
• D：

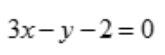
答 案：D

解 析：因为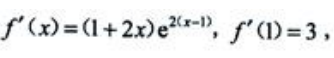则切线方程的斜率k＝3，x＝1，y＝1.故切线方程为y－1＝3（x－1），即3x－y－2＝0.

2、（）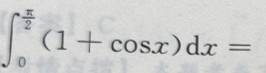

• A：
• B：
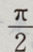
• C：
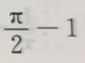
• D：1

答 案：A

解 析：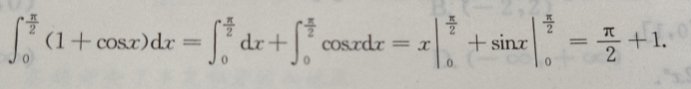

主观题

1、求由方程siny＋xe^y＝0确定的曲线在点（0，π）处的切线方程．

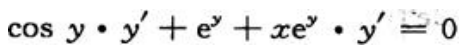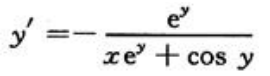答 案：解：方程两边对x求导得得所以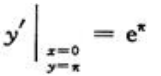,故所求切线方程为y－π＝e^π（x－0）,即e^πx－y＋π＝0

2、某射手击中10环的概率为0.26，击中9环的概率为0.32，击中8环的概率为0.36，求在一次射击中不低于8环的概率．

答 案：解：设A＝{击中10环），B＝{击中9环），C＝{击中8环），D＝{击中不低于8环），则D＝A＋B＋C，由于A，B，C相互独立，所以P（D）＝P（A＋B＋C）＝P（A）＋P（B）＋P（C）＝0.26＋0.32＋0.36＝0.94

填空题

1、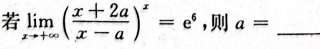

答 案：2

解 析：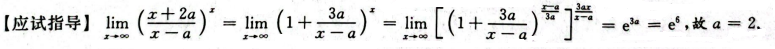

2、（）．

答 案：

解 析：因为积分区间关于原点对称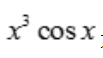，是奇函数，故，则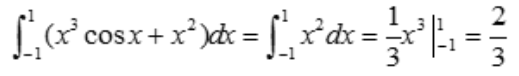

简答题

1、求函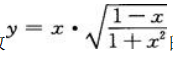数的倒数。  

答 案：等式两边同时取对数得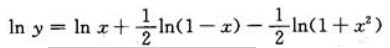 方程两边同时对x求导有 故

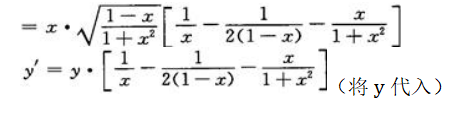
2、设y=x²·e^x，求y’。      

答 案：本题考查的知识点是函数乘积的导数计算。